Alternative Aggregate Combat Modeling
UAH, in collaboration with Gnosys Systems and SAIC, developed a new mathematical model of combat at the unit (aggregate) level. The model is based on detailed entity-level performance data but achieves the computational efficiency of a unit-level algorithm. Validation was conducted by comparing model results with actual outcome for a historical engagement.
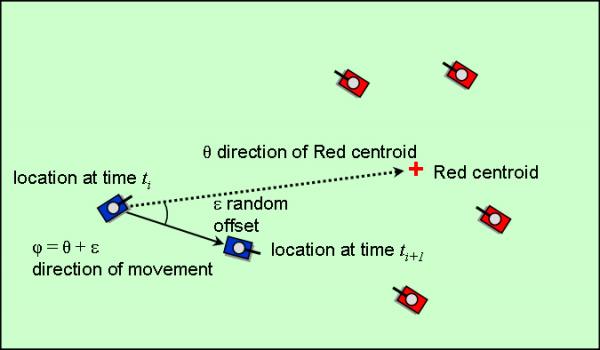
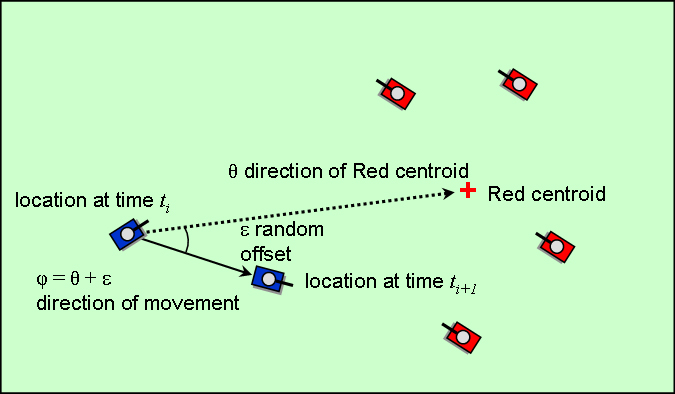
Unit-level combat models provide computational efficiency, with the result that they can simulate large scenarios in terms of geographic scope and size of military forces involved and are often able to execute much faster than real-time. However, existing unit-level combat models (such as Lanchester equations) don’t exploit the detailed performance data and high-fidelity models that are available at the entity level. In entity-level combat models combat phenomenology, such as moving, sensing, and shooting, is represented at entity level, which is both more intuitively acceptable to users and more directly supportable by available test and operational data on entity performance than the abstract equations of a unit-level model. However, current pure entity-level combat models tend to produce unrealistically high attrition. Under DARPA sponsorship, CMSA, Gnosys Systems, and SAIC have developed an alternative unit-level combat resolution algorithm. Within it the effects of moving, sensing, and shooting on unit-level combat outcome are based on entity-level performance information, directly supportable by test and operational data. Despite entity-level basis, the algorithm is sufficiently abstract to allow responsive execution in the context of a unit-level simulation. Entity-level performance is represented by a set of probability functions that eliminate as much entity level detail as possible while retaining the important effects of entity-level performance on combat outcome. These probability functions, all of which are based on entity-level data and models, include intervisibility, detection, kill, and location. The functions operate within equations that consider potential interactions between entity types and likely locations of entities of different types.