Low-Demand Inventory Stocking Strategies
Discrete event simulation provides optimization of inventory levels in the very low demand regime of Army Aviation. Preliminary results favor surprisingly simple stocking strategies in optimizing readiness vs. cost.
A simple question is how much stock one should hold on hand in anticipation of future need. Holding stock in inventory costs money, so a balance must be struck between the cost of inventory stock and the cost of unmet demand. The Inventory Analyst (IA) package has been successfully used and widely implemented to optimize stocking level for many industrial applications. Such applications typically involve hundreds to thousands of items. In this large-N regime, simple Gaussian (normal) statistics can be used to approximate the demand that may arise in a given stocking period. When demand is very low, however, Gaussian statistics fail for instance, negative demand is theoretically possible in a Gaussian distribution. Mathematical models based on the Gaussian model, therefore, produce results that are difficult to interpret. The optimal stocking may be 0.127 items; should one round up, to guarantee at least one part is present, or round down to minimize cost? The situation is further complicated in Army Aviation by the fact that some parts are regarded as critical, in the sense that a helicopter missing that part cannot fly at all. Other parts are regarded as non-critical. The optimum overall strategy likely uses different strategies for critical and non-critical parts.
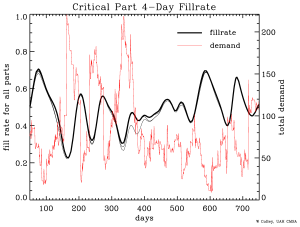
Our solution is a discrete event simulation, using first-in-first-out queues to represent the individual demands and the stocked instances for each part. As input, we use the historical record of Army Aviation parts ordered from the Korean theater in a roughly 750-day period beginning in 2003. We treat new stock arrivals, and new demands as occurring daily, with orders spending 42 days in transit from the continental United States. We have experimented with several different stocking strategies, such as rounding up, simple rounding, and rounding down of the IA solution, and similar rounding for a simple average 42-day demand (mean daily demand times 42 days, mean solution). The IA solution and mean solutions yield similar results, with slightly better readiness per stocking cost for the mean solution. Somewhat surprisingly rounding strategy makes little difference for readiness, but has a dramatic impact on cost. Also surprisingly, the IA solution underperforms with respect to readiness, though further work has shown that our understanding of the problem is limited by the input, which is historical track of orders, rather than demands. We have found that orders tend to peak dramatically after long periods of quiescence. Some of these peaks associate with Army fiscal cycles, and are likely spurious as indicators of actual demand. If a more plausible demand sequence, based on stochastic statistics, is adopted, the IA solution performs nearly nominally.